RAM

Jolt proves the correctness of RAM operations using the Twist memory checking algorithm, specifically utilizing the "local" prover algorithm.

Dynamic parameters

In Twist, the parameter $K$ determines the size of the memory. For RAM, unlike registers, $K$ is not known a priori and depends on the memory usage of the guest program. Consequently, the parameter $d$, dictating how the memory address space is partitioned into chunks, must also be dynamically tuned. This ensures that no committed polynomial exceeds a maximum size defined by $T\times K^{1/d}$.

Jolt is currently configured so that $K^{1/d}=2^8$.

Address remapping

We treat each 8-byte-aligned doubleword in the guest memory as one "cell" for the purposes of memory checking. Our RISC-V emulator is configured to use 0x80000000 as the DRAM start address -- the stack and heap occupy addresses above the start address, while Jolt reserves some memory below the start address for program inputs and outputs.

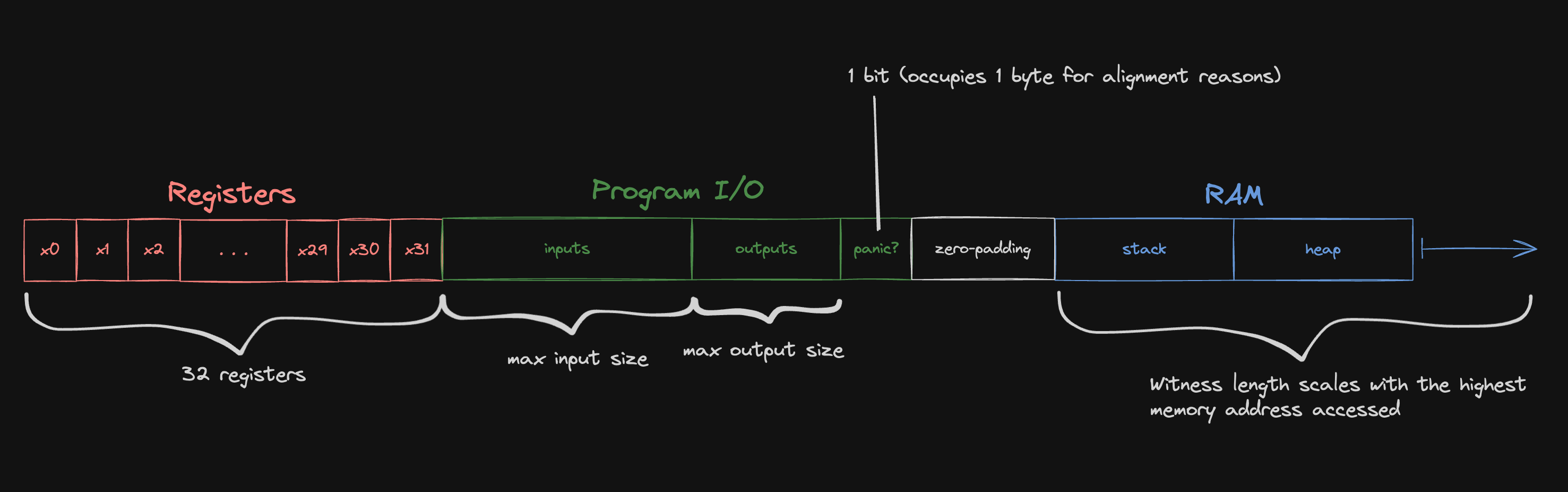
For the purposes of the memory checking argument, we remap the memory address to a witness index:

#![allow(unused)]
fn main() {
(address - memory_layout.lowest_address) / 8
}

where lowest_address is the left-most address depicted in the diagram above. The division by eight reflects the fact that we treat guest memory as "doubleword-addressable" for the purposes of memory-checking. Any load or store instructions that access less than a full doubleword (e.g. LB, SH, LW) are expanded into inline sequences that use the LD or SD instead.

Deviations from the Twist algorithm as described in the paper

Our implementation of the Twist prover algorithm differs from the description given in the Twist and Shout paper in a couple of ways. One such deviation is wv virtualization. Other, RAM-specific deviations are described below.

Single operation per cycle

The Twist algorithm as described in the paper assumes one read and one write per cycle, with corresponding polynomials $\widetilde{\text{ra}}$ (read address) and $\widetilde{\text{wa}}$ (write address). However, in the context of the RV64IMAC instruction set, only a single memory operation -- either a read or a write (or neither) -- is performed per cycle. Thus, a single polynomial (merging $\widetilde{\text{ra}}$ and $\widetilde{\text{wa}}$) suffices, simplifying and optimizing the algorithm. This polynomial is referred to as $\widetilde{\text{ra}}$ for the rest of this document.

No-op cycles

Many instructions do not access memory, so we represent them using a row of zeros in the $\widetilde{\text{ra}}$ polynomial rather than the one-hot encoding of the accessed address. Having more zeros in $\widetilde{\text{ra}}$ makes it cheaper to commit to and speeds up some of the other Twist sumchecks. This modification necessitates adjustments to the Hamming weight sumcheck, which would otherwise enforce that the Hamming weight for each "row" in $\widetilde{\text{ra}}$ is 1.

We introduce an additional Hamming Booleanity sumcheck:

$$0=\sum _{j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r^{\prime },j)\cdot \left(\widetilde{\text{hw}}(j{)}^2-\widetilde{\text{hw}}(j)\right)$$

where $\widetilde{\text{hw}}$ is the Hamming weight polynomial, which can be virtualized using the original Hamming weight sumcheck expression:

$$\widetilde{\text{hw}}(r_{\text{cycle}})=\sum _{k=(k_1,\dots ,k_d)\in {\left(\{0,1{\}}^{\log (K)/d}\right)}^d}\widetilde{\text{ra}}(k,r_{\text{cycle}})$$

For simplicity, these equations are presented for the $d=1$ case, but as described above, $d$ for RAM is dynamic and can be greater than one.

ra virtualization

In Twist as described in the paper, a higher $d$ parameter would translate to higher sumcheck degree for the read checking, write checking, and $\widetilde{\text{raf}}$ evaluation sumchecks. Moreover, $d>1$ is fundamentally incompatible with the local prover algorithm for the read/write checking sumchecks.

To leverage the local algorithm while still supporting $d>1$, Jolt simply carries out the read checking, write checking, and $\widetilde{\text{raf}}$ evaluation sumchecks as if $d=1$, i.e. with a single (virtual) $\widetilde{\text{ra}}$ polynomial.

At the conclusion of these sumchecks, we are left with claims about the virtual $\widetilde{\text{ra}}$ polynomial. Since the polynomial is uncommitted, Jolt invokes a separate sumcheck that expresses an evaluation $\widetilde{\text{ra}}$ in terms of the constituent ${\widetilde{\text{ra}}}_i$ polynomials. The ${\widetilde{\text{ra}}}_i$ polynomials are, by definition, a tensor decomposition of $\widetilde{\text{ra}}$, so the "ra virtualization" sumcheck is the following:

$$\widetilde{\text{ra}}(r,r^{\prime })=\sum _{j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r^{\prime },j)\cdot \left(\prod _{i=1}^d{\widetilde{\text{ra}}}_i(r_i,j)\right)$$

Advice Inputs

The $\widetilde{\text{Val}}$ evaluation sumcheck in Twist requires both the prover and verifier to know the initial state of the lookup table. When advice inputs are present in the RAM lookup table, the verifier doesn't have direct access to these values. To address this, the prover provides evaluations of the advice inputs and later proves their correctness against commitments held by the verifier.

For trusted advice, the commitment is generated externally; for untrusted advice, the prover generates the commitment. All advice inputs are placed at the lowest addresses of the RAM lookup table, with the larger advice type placed first to minimize field multiplications during verification.

We represent advice inputs and the RAM lookup table as multi-linear polynomials, assuming their sizes are powers of two.

Let:

• ${\widetilde{\text{ram}}}_{\text{init-p}}(k)$ be the prover's RAM lookup table polynomial (including advice)
• ${\widetilde{\text{ram}}}_{\text{init-v}}(k)$ be the verifier's RAM lookup table polynomial (zeros in advice section, otherwise identical to prover's)
• $\widetilde{\text{trusted}}(m)$ be the trusted advice polynomial
• $\widetilde{\text{untrusted}}(n)$ be the untrusted advice polynomial

where $m\ge n$ (if this condition isn't met, we reorder the advice types to ensure the larger one comes first).

Let $i$ be the position of the single set bit in $(m+n)/m$ within its $\log k$-bit representation. This position corresponds to bit $\log m$ when $n<m$, or $\log m+1$ when $n=m$.

The relationship between these polynomials is:

$${\widetilde{\text{ram}}}_{\text{init-p}}(k)={\widetilde{\text{ram}}}_{\text{init-v}}(k)+\left(\prod _{j=0}^{\log k-\log m-1}(1-k_j)\right)\cdot \widetilde{\text{trusted}}(k_{\log k-\log m},\dots ,k_{(\log k)-1})+\left(\prod _{j=0,j\ne i}^{\log k-\log n-1}(1-k_j)\right)\cdot k_i\cdot \widetilde{\text{untrusted}}(k_{\log k-\log n},\dots ,k_{(\log n)-1})$$

Since the verifier only needs to evaluate ${\widetilde{\text{ram}}}_{\text{init-p}}$ at a random point, it can compute this value efficiently using ${\widetilde{\text{ram}}}_{\text{init-v}}$ and the evaluations of the trusted and untrusted components.

Example

Consider a concrete example with:

• Total memory: 8192 elements ($2^{13}$)
• Trusted advice: 1024 elements ($2^{10}$)
• Untrusted advice: 128 elements ($2^7$)

The memory layout would be:

• Addresses with the 3 MSBs as 000: trusted advice region (all combinations of the remaining 10 bits)
• Addresses with the MSBs as 001000: untrusted advice region (all combinations of the remaining 7 LSBs)

This arrangement minimizes verifier computation. If we placed untrusted advice first, the verifier would need to check multiple bit patterns (000001, 000010, etc.) for the trusted section, resulting in significantly more field multiplications.

Output Check

Jolt ensures correctness of guest program outputs via the output check sumcheck. Guest I/O operations, including outputs, inputs, and termination or panic bits, occur within a designated memory region. At execution completion, outputs and relevant status bits are written into this region.

Verifying that the claimed outputs and status bits are correct amounts to checking that the following polynomials agree at the indices corresponding to the program I/O memory region:

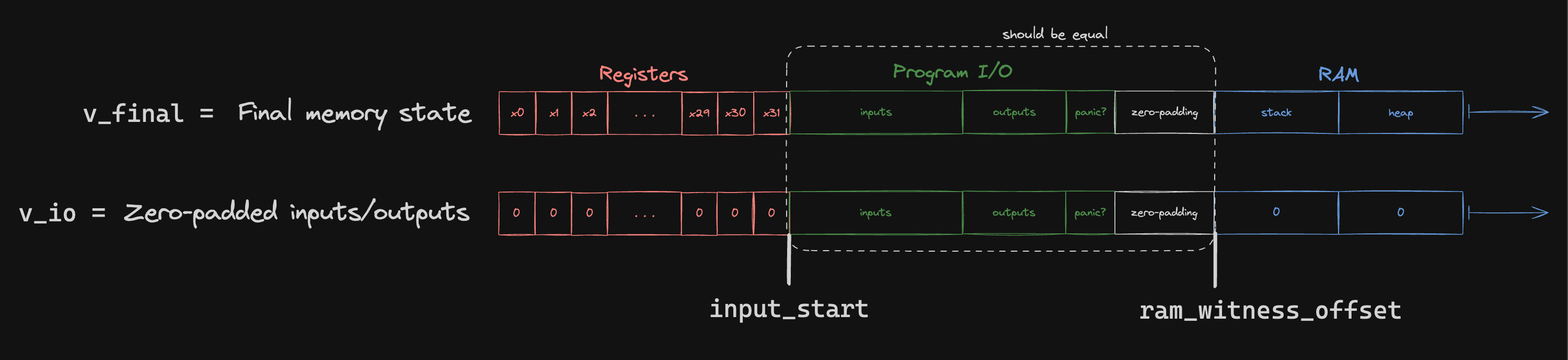
Note that val_io is only contains information known by the verifier. To check that these two polynomials are equal, we use the following sumcheck:

$$0=\sum _{k\in \{0,1{\}}^{\log K}}\widetilde{\text{eq}}(r_{\text{address}},k)\cdot \widetilde{\text{io-range}}(k)\cdot \left({\widetilde{\text{Val}}}_{\text{final}}(k)-{\widetilde{\text{Val}}}_{\text{io}}(k)\right)$$

where $\widetilde{\text{io-range}}$ is a "range mask" polynomial, equal to 1 at all the indices corresponding to the program I/O region and 0 elsewhere. The MLE for a range mask polynomial that isolates the range $[\text{start},\text{end})$ can be written as follows:

$${\widetilde{\text{mask}}}_{\text{start, end}}(r)=\widetilde{\text{LT}}(r,\text{end})-\widetilde{\text{LT}}(r,\text{start})$$

It is implemented in code as RangeMaskPolynomial.

This output check sumcheck generates a claim about the final memory state polynomial (${\widetilde{\text{Val}}}_{\text{final}}$), which, being virtual, is proven using the ${\widetilde{\text{Val}}}_{\text{final}}$ evaluation sumcheck:

$${\widetilde{\text{Val}}}_{\text{final}}(r)-{\widetilde{\text{Val}}}_{\text{init}}(r)=\sum _{j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{Inc}}(j)\cdot \widetilde{\text{ra}}(r,j)$$

Intuitively, the delta between the final and initial state of some memory cell is the sum of all increments to that cell.

The verifier also requires evaluations of the advice sections to compute ${\widetilde{\text{Val}}}_{\text{init}}$. As with the $\widetilde{\text{Val}}$ evaluation described above, the prover provides these evaluations. Since both sumchecks use the same randomness, the prover only needs to provide one evaluation proof per advice type. If different randomness were used, separate proofs would be required for each sumcheck.

You may have noticed in the above expression that $\widetilde{\text{Inc}}(j)$ if a polynomial only over cyclce variables, while the book describes $\widetilde{\text{Inc}}:{\mathbb{F}}^{\log K}\times {\mathbb{F}}^{\log T}\to \mathbb{F}$. This change is explained in wv virtualization.

Both the ${\widetilde{\text{Val}}}_{\text{final}}$ and $\widetilde{\text{Val}}$ evaluation sumchecks use the virtual $\widetilde{\text{ra}}$ polynomial, with claims subsequently proven via ra virtualization sumcheck.