Twist and Shout

🚧 These docs are under construction 🚧

👷If you are urgently interested in this specific page, open a Github issue and we'll try to expedite it.👷

One-hot polynomials

A one-hot vector of length $n$ is a unit vector in $$\begin{gathered} {0,1 \\ }^n \end{gathered}$$, i.e., a vector of length $n$ with exactly one entry equal to $1$ and all other entries equal to $0$.

In Jolt, we refer to the multilinear extension (MLE) of a one-hot vector as a one-hot polynomial.

We also use the same terminology to refer to the concatenation of $T$ different one-hot vectors. For example, if $$\begin{gathered} y=(y_1,\dots ,y_T)\in {\left( \\ {0,1 \\ }^n\right)}^T \end{gathered}$$ where each $y_i$ is one-hot, then we'll call $y$ one-hot, and say the same about its MLE.

Shout

Shout is a batch-evaluation argument. Let $$\begin{gathered} f: \\ {0,1 \\ }^n\to \mathbf{F} \end{gathered}$$ be any function, and suppose the prover has already committed to $T$ inputs $x_1,\dots ,x_T$ to $f$. A batch-evaluation argument gives the verifier query access to the MLE of the output vector $(f(x_1),\dots ,f(x_T))$.

From the verifier's perspective, a batch-evaluation argument is an efficient reduction from the difficult task of evaluating the MLE of the output vector $(f(x_1),\dots ,f(x_T))$ at a random point, to the easier task of evaluating the MLE of the input vector $x=(x_1,\dots ,x_T)$ at a random point.

In Shout, a wrinkle is that each input $x_i$ to $f$ is committed in one-hot form (i.e., as a unit vector in $$\begin{gathered} {0,1 \\ }^{2^n} \end{gathered}$$) rather than as a binary vector in $$\begin{gathered} {0,1 \\ }^n \end{gathered}$$. For example, if $n=2$, $T=2$, $x_1=(1,0)$ and $x_2=(1,1)$, then in Shout $x_1$ will be committed as the length-four unit vector $(0,0,1,0)$ while $x_2$ will be committed as $(0,0,0,1)$.

Let $F$ denote the evaluation table of $F$, i.e., $F$ is the vector of length $2^n$ whose $k$'th entry stores $f(k)$. Let $\mathsf{ra}(j,k)$ denote the matrix whose $j$'th row is the one-hot representation of vector $x_j$.

Then $f(x_j)$ is simply the inner product of row $j$ of $\mathsf{ra}$ with $F$. This can be seen to imply that for any $(r_1,\dots ,r_{\log T})\in {\mathbb{F}}^{\log T}$, $$\begin{gathered} \tilde{y}(r_1,\dots ,r_{\log T})=\sum _{k\in \\ {0,1 \\ }^n}\widetilde{\mathsf{ra}}(k,r_1,\dots ,r_{\log T})\tilde{f}(k). \end{gathered}$$

All that Shout does is apply the sum-check protocol to compute the above sum. From the verifier's perspective, this reduces the task of computing $\tilde{y}(r_1,\dots ,r_{\log T})$ to that of evaluation $\tilde{f}$ at a random point and evaluation $\widetilde{\mathsf{ra}}$ at a random point. Since the vector $\widetilde{\mathsf{ra}}$ was committed by the prover, the prover can provide the requested evaluation of $\widetilde{\mathsf{ra}}$ along with an evaluation proof.

In the case where committing to, or providing an evaluation proof for, $\mathsf{ra}$ is too expensive, Shout instead virtualizes $\mathsf{ra}$. This means $\mathsf{ra}$ itself is not committed. Rather, several smaller vectors are committed, and when the verifier needs to evaluate $\mathsf{ra}$ at a random point, the sum-check protocol is applied to reduce evaluating (the MLE of) $\mathsf{ra}$ at a point to evaluating (the MLEs of) the simpler vectors at a different point.

In Shout, this virtualization uses the fact that, since (each of the $T$ rows of) $u$ is one-hot and of length $n$ , (each row of) $u$ can be expressed as the tensor product of $d$ smaller one-hot vectors, each of length $2^{n/d}$. Rather than committing to $u$ directly, the prover commits to the $d$ smaller vectors, and then we use an additional application of the sum-check protocol to reduce the task of evaluating $\widetilde{\mathsf{ra}}$ at a point to the task of evaluation each of the $d$ smaller vectors at a point.

Prefix-suffix Shout

For the Shout verifier to be fast, all that is needed is that $\tilde{f}$ be quickly evaluable. This is the case for all of the primitive RISC-V instructions (and many other functions). However, for the Shout prover to be fast, $f$ needs additional structure. We call the kind of structure exploited to make the Jolt prover fast prefix-suffix structure. Prefix-suffix structure is spiritually similar to the notion of decomposable tables in Lasso: roughly, it captures the situation where a single evaluation of $f$ at input $$\begin{gathered} x\in \\ {0,1 \\ }^n \end{gathered}$$ can be obtained by splitting $x$ into $c$ chunks each of size $n/c$, evaluating a simple function on each chunk, and putting the evaluations together in a simple way. Whereas the Lasso prover had to explicitly commit to the chunks, the Shout prover only uses the decomposition ``in its own head'' to compute its sum-check messages quickly. This is one reason the Shout protocol is much more efficient than the Lasso protocol: table decompositions are not baked into the protocol itself but rather used only by the prover to quickly compute sum-check messages. The protocol itself is agnostic to the decomposition used (and in particular does not force the prover to use a particular decomposition).

For details, see Appendix A of [NTZ25].

Twist

Shout is a batch-evaluation argument, which can equivalently be viewed as a lookup argument, i.e., for performing reads into a read-only memory. The relevant read-only memory for Shout is the memory that stores all $2^n$ evaluations of the function $f$ being evaluated.

Twist is an extension from read-only memory to read-write memory.

Imagine the prover has already committed to $T$ read addresses and $T$ write addresses, each address indexing into a memory of size $K$. The prover has also committed to a \emph{value} associated with each write operation. We think of reads and writes as proceeding in ``cycles'' (analogous to CPU cycle), where in each cycle $j$, the $j$'th read operation happens, followed by the $j$'th write operation.

The goal of Twist is to give the verifier query access to (the MLE of) the vector $\text{rv}$ of read-values, where $\text{rv}(j)$ denotes the value returned by the $j$'th read operation (i.e., the value that, as of time $j$, was most recently written to the $j$'th read address).

In Twist, as in Shout, each address is specified in one-hot form. So we think of the read addresses as a matrix $\text{ra}$ whose $j$'th row is the one-hot representation of the address read at cycle $j$, and similarly for write address $\text{wa}$.

Whereas Shout involves a single invocation of the sum-check protocol (plus an additional invocation if $\mathsf{ra}$ is virtualized in terms of smaller vectors), Twist involves several invocations of the sum-check protocol. We call these the read-checking sum-check, the write-checking sum-check, and the Val-evaluation sum-check.

Prior to the start of these three invocations of the sum-check protocol, the Twist prover commits to a vector called the Increments vector, or $\text{Inc}$ for short. If $k$ is the cell written at cycle $j$, then $\text{Inc}(j)$ returns the difference between the value written in cycle $j$ and the stored at cell $k$ at the start of the cycle. The next section explains that once $\text{Inc}$ is committed, there is actually no need to commit to the write values $\text{wv}$: the $j$'th write value is in fact implied by the associated increment, so there is no need to commit to both.

wv virtualization

In the Twist and Shout paper (Figure 9), the read and write checking sumchecks of Twist are presented as follows:

Observe that the write checking sumcheck is presented as a way to confirm that an evaluation of $\widetilde{\text{Inc}}:{\mathbb{F}}^{\log K}\times {\mathbb{F}}^{\log T}\to \mathbb{F}$ is correct.

Under this formulation, both $\widetilde{\text{Inc}}$ and the $\widetilde{\text{wv}}:{\mathbb{F}}^{\log T}\to \mathbb{F}$ polynomial are committed.

With a slight tweak, we can avoid committing to $\text{wv}$. First, we will modify $\widetilde{\text{Inc}}$ to be a polynomial over just the cycle variables, i.e. $\widetilde{\text{Inc}}:{\mathbb{F}}^{\log T}\to \mathbb{F}$. Intuitively, the $j$th coefficient of $\widetilde{\text{Inc}}$ is the delta for the memory cell accessed at cycle $j$ (agnostic to which cell was accessed).

Second, we will reformulate the write checking sumcheck to more closely match the read checking sumcheck:

$$\widetilde{\text{wv}}(r^{\prime })=\sum _{k=(k_1,\dots ,k_d)\in {\left(\{0,1{\}}^{\log (K)/d}\right)}^d,j\in \{0,1{\}}^{\log (T)}}\widetilde{\text{eq}}(r,k)\cdot \widetilde{\text{eq}}(r^{\prime },j)\cdot \left(\left(\prod _{i=1}^d{\widetilde{\text{wa}}}_i(k_i,j)\right)\cdot \left(\widetilde{\text{Val}}(k,j)+\widetilde{\text{Inc}}(j)\right)\right)$$

Intuitively, the write value at cycle $j$ is equal to whatever was already in that register ($\widetilde{\text{Val}}(k,j)$), plus the increment ($\widetilde{\text{Inc}}$).

We also need to tweak the $\widetilde{\text{Val}}$-evaluation sumcheck to accommodate the modification $\widetilde{\text{Inc}}$. As presented in the paper:

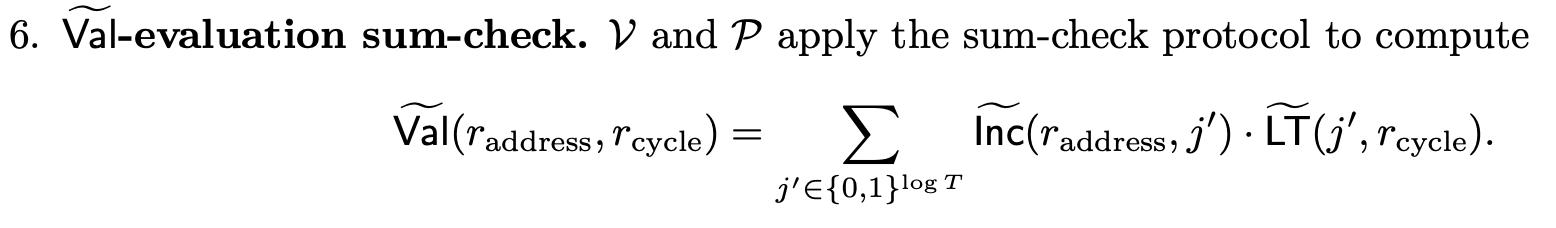
After modifying $\widetilde{\text{Inc}}$ to be a polynomial over just the cycle variables:

$$\widetilde{\text{Val}}(r_{\text{address}},r_{\text{cycle}})=\sum _{j^{\prime }\in \{0,1{\}}^{\log T}}\widetilde{\text{Inc}}(j^{\prime })\cdot \widetilde{\text{wa}}(r_{\text{address}},j^{\prime })\cdot \widetilde{\text{LT}}(j^{\prime },r_{\text{cycle}})$$